Tag: PWR

Weekly UND PWR outlook

In this idle weekend, #2 UND (PairWise Rankings) is most likely to keep its #2 ranking, but if they move it will probably be down to #3.

UND_Feb9

 

That .7% chance of UND taking #1 is largely the likelihood of Alaska-Anchorage sweeping Minnesota State (KRACH gives Anchorage a ranking of 53.43 and Minnesota State a ranking of 613.98, thus predicting Alaska-Anchorage has an 8% chance of winning each game, or about a .6% chance of winning both).

To see the threat of falling to #3, UND need only look at current #3 Boston University. UND currently wins the comparison 2-0, but on a razor thin .5856-.5845 RPI advantage. Even a single BU win (and a few other things going right) could be enough for BU to overtake UND.

End of regular season outlook

The regular season outlook has improved to the point that UND is nearly a lock for an at-large bid. Only an epic collapse (e.g. 2 or fewer wins in the final 8 games) combined with a disastrous conference tournament could knock UND out.

UND_endofseason

Can UND take over #1 this weekend?

It’s a bit of a longshot, but if everything goes well for UND this weekend, they could climb to #1 in the PairWise Rankings. Incumbent Minnesota State controls it’s own destiny — a sweep guarantees they stay atop the heap for one more week. A split, however, opens the door for UND.

mankato

If UND sweeps, they can take #1 with a suitably bad performance by Mankato. It’s remotely possible, though not likely, for North Dakota to take #1 even with a split.

NorthDakota

Finally, it’s remotely possible (about 2%) for Nebraska-Omaha to take the #1 spot this weekend (a scenario that would almost certainly require a sweep of UND), and extremely remotely possible (about .2%) for Boston University to take #1.

UND’s PWR rankings — a look ahead

Last week I gave a quick preview of UND’s PWR chances for the weekend. After a tie and a win, UND landed about where expected at #19. However, UND still has good upside potential.

UND’s one week outlook

A sweep should move UND solidly into “at large” position, while a split would leave UND about where it is (with a slight improvement a bit more likely than a slight fall).

UND’s regular season outlook

The bigger picture, though, is after UND’s phenomenal lossless streak, what do they need to do to finish in charge of their own destiny?

Winning 8 of its remaining 12 would put UND in a decent position to make the playoffs at large, while only winning 6 would likely leave UND in need of some conference tournament success.

More PWR analysis (non-UND teams)

I’m pleased to announce a new web site, College Hockey Ranked, to which I’ll (slowly) be migrating the non-UND hockey ranking information. This will allow SiouxSports to refocus more tightly on being a destination for UND fans, while CollegeHockeyRanked will try to appeal to a more general college hockey audience. UND fans who just want to read about UND won’t have to sift through as much information about other teams (except as it pertains to UND), non-UND fans who want more general analysis won’t have to skip over UND-centric analysis if they just visit that site, and of course anyone interested in both can simply follow both sites.

The immediate impact of this shift is that I’ll start posting my non-UND analysis to articles on that site. At least for this season, though, I’ll probably link between the two a lot.

Methodology

Each forecast is based on at least one million monte carlo simulations of the games in the described period. For each simulation, the PairWise Ranking (PWR) is calculated and the results tallied. The probabilities presented in the forecasts are the share of simulations in which a particular outcome occurred.

The outcome of each game in each simulation is determined by random draw, with the probability of victory for each team set by their relative KRACH ratings. So, if the simulation set included a contest between team A with KRACH 300 and team B with KRACH 100, team A will win the game in very close to 75% of the simulations. I don’t simulate ties or home ice advantage.

Resources

First look at UND’s Pairwise chances

I’ll go into some more depth in future weeks, but here’s a sneak preview of PairWise Ranking prognostication for the season–

This would have been a lot more interesting a month ago when UND seemed at serious risk of a lost season and I could have said something like, “UND needs to win the next 7 just to climb up to 20th”. Here we are at #19 with 14 regular season NCAA games remaining, and UND is definitely back in the hunt.

Here’s how this weekend’s games could affect its PWR:

The first thing that jumped out at me is how huge the spreads are — UND’s median climb for a sweep is 5 positions and fall for getting swept is 7. It appears that UND is just at a dense part of the RPI, but given that the PWR formula is new this year I’ll try to do some more digging.

Best of three weekend Pairwise possibilities

This is the last week we look at single week ranking probabilities, after this the “You are the Committee” calculators will go live and we’ll give you the rundown on all remaining possible outcomes.

It’s an interesting week, with a lot of teams’ fortunes still at play.

While the first three (#1 Quinnipiac, #2 Minnesota, and #3 Miami) in the Pairwise Rankings are reasonably secure, it starts to get interesting at #4 Mass.-Lowell. The Riverhawks are likely to stay #4-5 if they emerge from the best of 3, but plummet if they get eliminated.

The same holds true for #5 North Dakota, #6 Denver, and #7 Boston College.

#8 New Hampshire is the first team with serious upside potential. It has a decent RPI and TUC record and is playing a fellow team under consideration, Providence. Most surprisingly, the Wildcats don’t drop much this weekend if they get eliminated (particularly if they win one).

#9 Mankato, #10 Western Michigan, #11 Yale, #12 St Cloud St, and #13 Niagara all have the opportunity to climb with success, or fall to the bubble if eliminated.

#14 Rensselaer is the highest ranked team that could fall definitively below the bubble if swept.

#15 Notre Dame, #16 Union, and #17 Boston University can all push themselves onto the bubble with success this weekend.

#18 Wisconsin can put itself into a good position but is unlikely to quite climb onto the bubble even with a sweep this weekend.

#22 Alaska is the highest ranked team not playing this weekend. Though incredibly unlikely (<1% chance), they could mathematically still climb onto the bubble.

#25 Air Force is the cutoff beyond which even active teams don’t seem to be able to climb onto the bubble through this weekend’s performance alone.

If there’s anything else you’d like to know (e.g. what games are most important for a particular team, what are the chances for a team note listed here), just let me know in the comments!

Methodology

Each forecast is based on at least one million monte carlo simulations of the games in the described period. For each simulation, the PairWise Ranking (PWR) is calculated and the results tallied. The probabilities presented in the forecasts are the share of simulations in which a particular outcome occurred.

The outcome of each game in each simulation is determined by random draw, with the probability of victory for each team set by their relative KRACH ratings. So, if the simulation set included a contest between team A with KRACH 300 and team B with KRACH 100, team A will win the game in very close to 75% of the simulations. I don’t simulate ties or home ice advantage.

Resources

UND needs wins to maintain its lofty ranking

#5 UND has climbed its way back into needing a sweep this weekend just to maintain its current ranking (Current PWR rankings).

Looking at UND’s PWR comparison details, NoDak has very limited upside potential this week. Only the Boston College comparison is obviously within reach, but UND is already ahead of BC in the ranking because of the RPI tie-breaker, so flipping that comparison may not even result in a ranking increase.

UND’s PWR comparisons and RPI details reveal a significant downside, however. The RPI value of winning these games is only .5784, not significantly different enough from UND’s RPI of .5455 to budge it much. The RPI value of losing is .3284, enough to drag down UND’s RPI a fair amount. The PWR comparison details reveal that UND is winning a number of comparisons only by a slim RPI lead (Naigara .5427, Mass.-Lowell .5448, Western Michigan .5384, St Cloud St .5412, and Dartmouth .5216).

Weekend games with the largest effect on UND’s PWR:

Outcome Number of
games		 Average effect
on UND’s PWR
North Dakota over Bemidji State (2 of 2) 4.60
North Dakota over Bemidji State (1 of 2) 2.17
Merrimack over Mass.-Lowell (2 of 2) 1.05
Providence over Boston College (2 of 2) 1.05
Merrimack over Mass.-Lowell (1 of 2) 0.93
Air Force over Niagara (2 of 2) 0.92
Air Force over Niagara (1 of 2) 0.73
Alaska Anchorage over Alaska (2 of 2) 0.70

I did a minimum quick update on UND this week because I’m a little late and last week’s UND closes in on NCAA tournament berth was so comprehensive. However, if there’s anything else you’d like to see or any particular questions you have, just let me know!

Methodology

Each forecast is based on at least one million monte carlo simulations of the games in the described period. For each simulation, the PairWise Ranking (PWR) is calculated and the results tallied. The probabilities presented in the forecasts are the share of simulations in which a particular outcome occurred.

The outcome of each game in each simulation is determined by random draw, with the probability of victory for each team set by their relative KRACH ratings. So, if the simulation set included a contest between team A with KRACH 300 and team B with KRACH 100, team A will win the game in very close to 75% of the simulations. I don’t simulate ties or home ice advantage.

Resources

UND closes in on NCAA tournament berth

#6 UND has moved much closer to clinching a tournament berth. Winning at least 2 of the remaining 6 would have UND more likely than not in the top 13 in PWR going into the conference tournaments. Even if UND won only 0 or 1 of its remaining games, an at large berth would still be within reach with a good showing in the conference tournament.

Given the above, UND faces a somewhat predictable situation this week of being able to make a small gain with a sweep over Denver, stay pretty much the same with a split, or fall a bit more if swept.

The final weeks of the regular season

Only three teams can’t fall from being a TUC by the end of the regular season: #1 Quinnipiac, #2 Minnesota, and #3 Miami.

Quinnipiac (PWR Details) is particularly safe, even a catastrophe seems to only drop them 3 spots. Winning only 2 of their remaining 4 would leave them with only about a 10% chance of falling from the #1 spot. Their .7778 vs. TUCs is unassailable, and .5828 RPI is miles ahead of #2 Minnesota .5658. To put that RPI into perspective, if Minnesota swept its final 6 games their RPI would only rise to about .5738 (Minnesota RPI details).

#2 Minnesota and #3 Miami each also have good RPI leads over the teams chasing them, coming in at .5658 and .5529 respectively, with #4 New Hampshire at .5477.

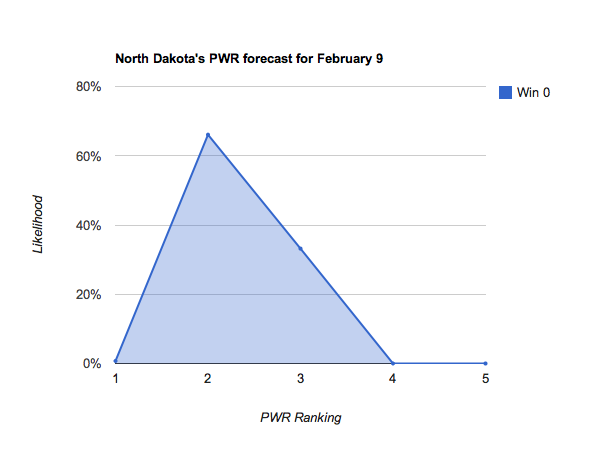
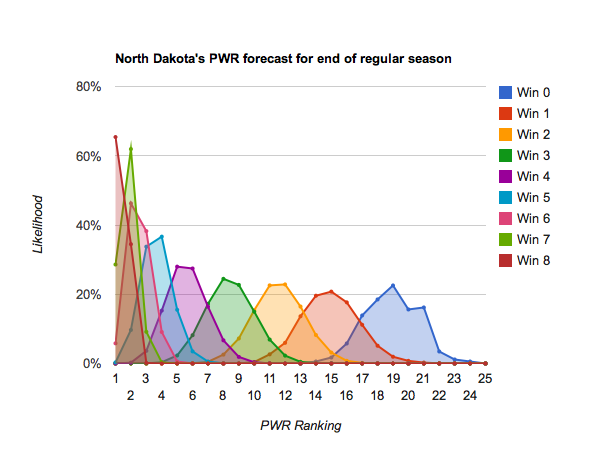
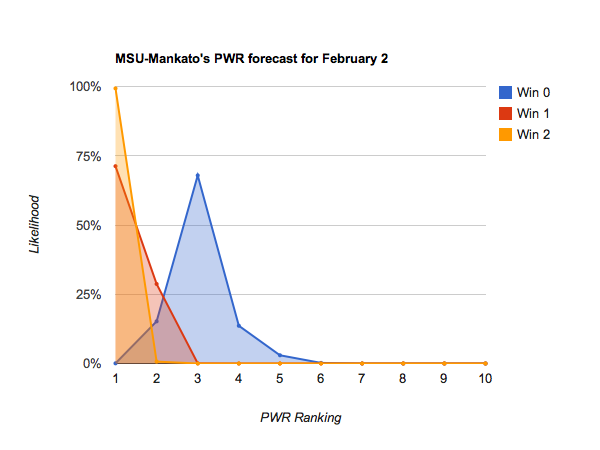
However, #2 Minnesota and #3 Miami aren’t alone in vying for the #2 PWR ranking at the end of the regular season. A staggering 9 teams could claim that position: #2 Minnesota, #3 Miami, #4 New Hampshire, #5 Boston College, #6 North Dakota, #7 MSU-Mankato, #9 St. Cloud St, #11 Denver, and #14 Mass.-Lowell.

Interestingly, the list of teams that can finish top 4 isn’t much longer, add only #8 Western Michigan and #10 Niagara to the list.

The team with the most upside potential for the remaining regular season is #29 Providence, which can climb to #8. That’s mostly just because big upward moves are possible from that low a rank (#28 Colgate and #30 Colorado College could each rise to #14).

The team with the most downside potential for the remaining regular season is #13 Boston University (BU PWR details), which could fall to not being a TUC. #13 BU is only #20 in RPI, and is already losing most of its common opponents comparisons.

Methodology

Each forecast is based on at least one million monte carlo simulations of the games in the described period. For each simulation, the PairWise Ranking (PWR) is calculated and the results tallied. The probabilities presented in the forecasts are the share of simulations in which a particular outcome occurred.

The outcome of each game in each simulation is determined by random draw, with the probability of victory for each team set by their relative KRACH ratings. So, if the simulation set included a contest between team A with KRACH 300 and team B with KRACH 100, team A will win the game in very close to 75% of the simulations. I don’t simulate ties or home ice advantage.

Resources

Small rankings moves likely for UND in bye week

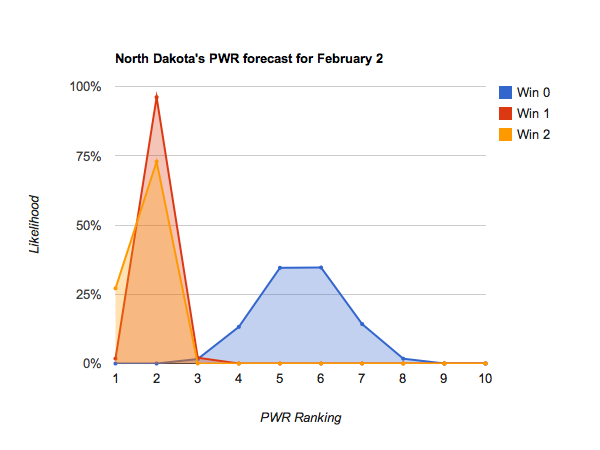
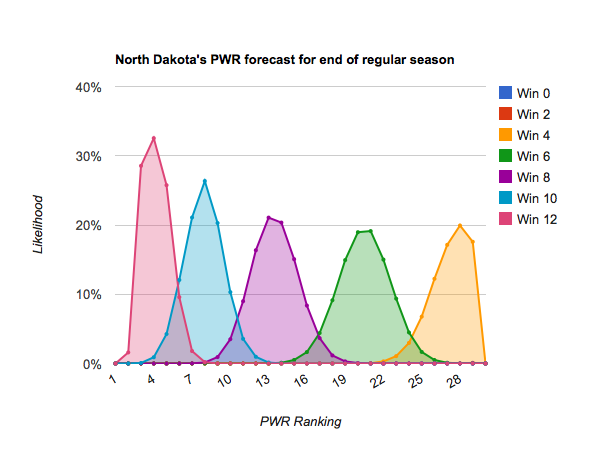
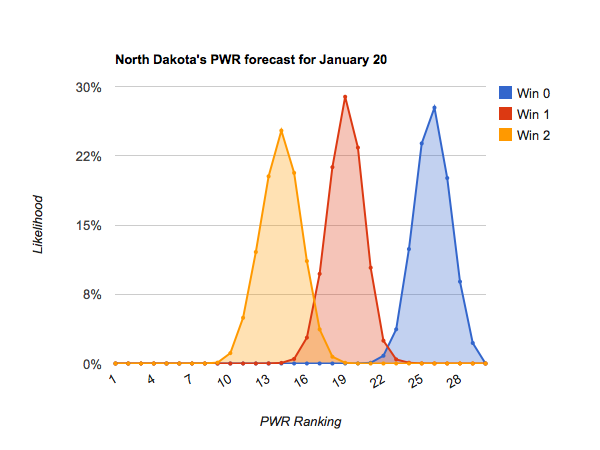
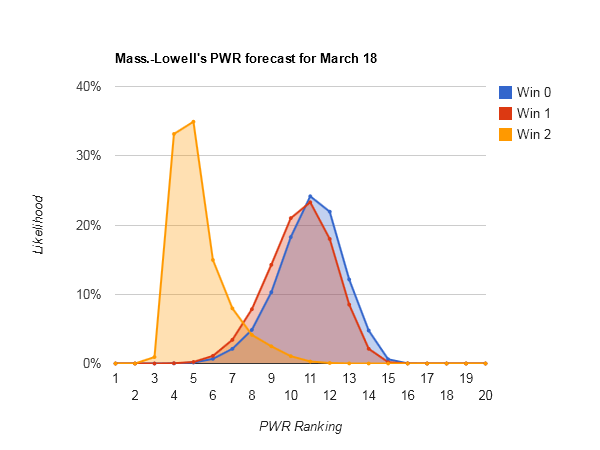
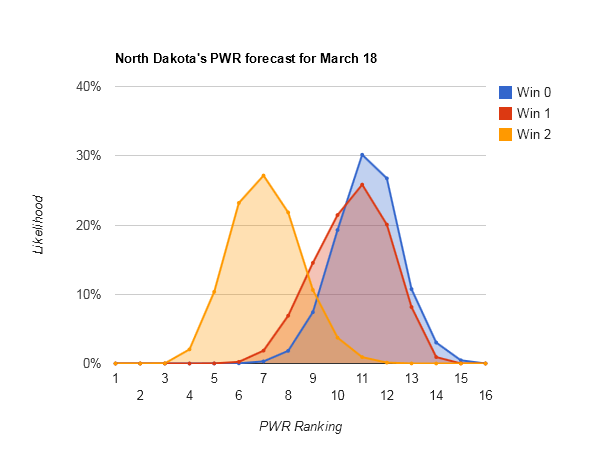
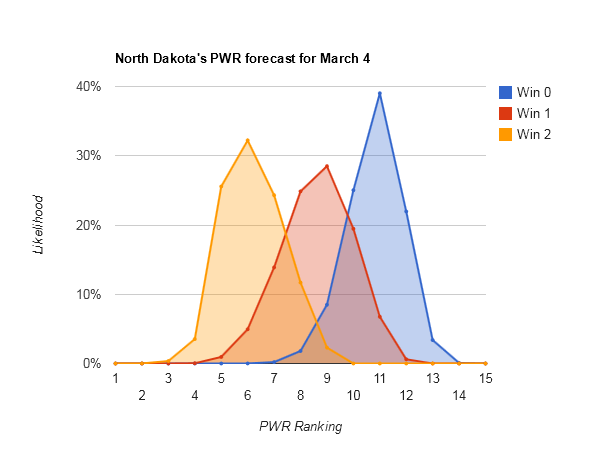
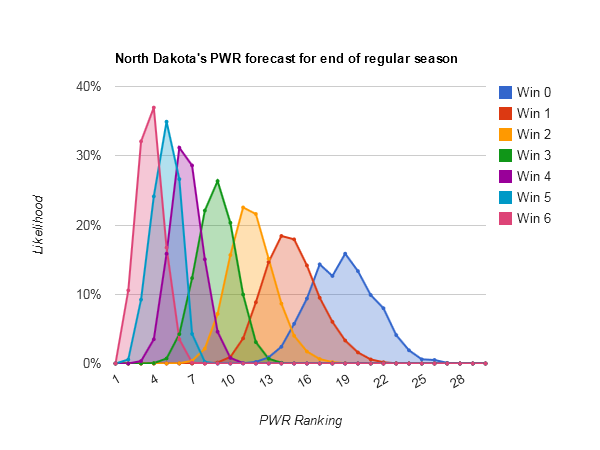
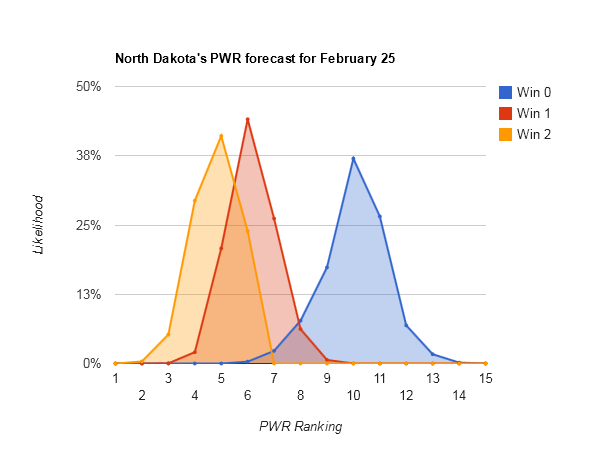
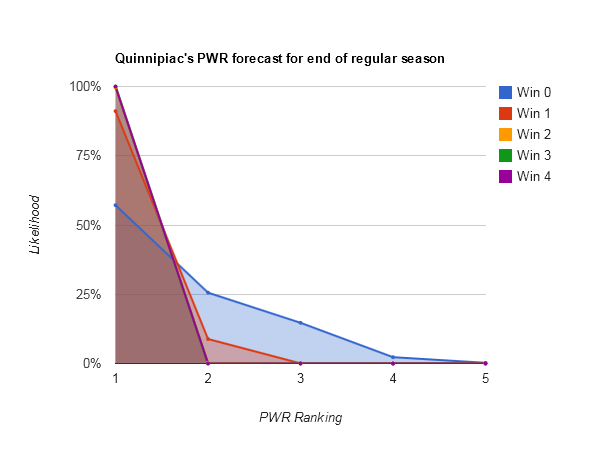
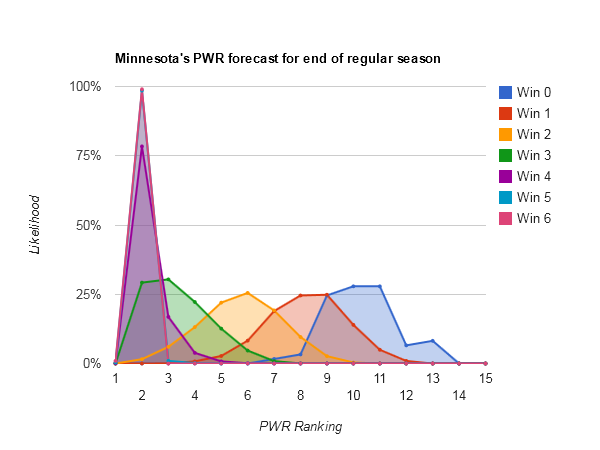
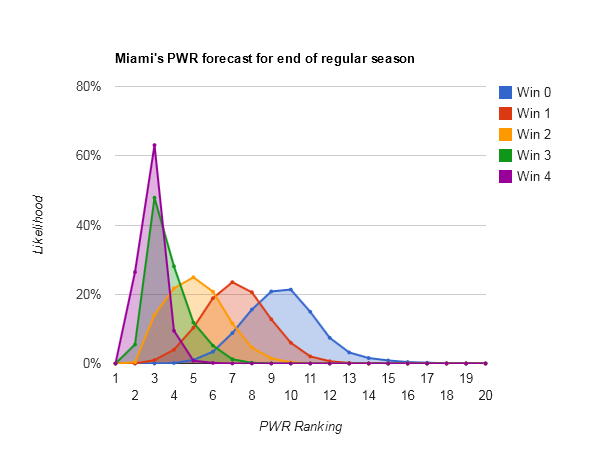
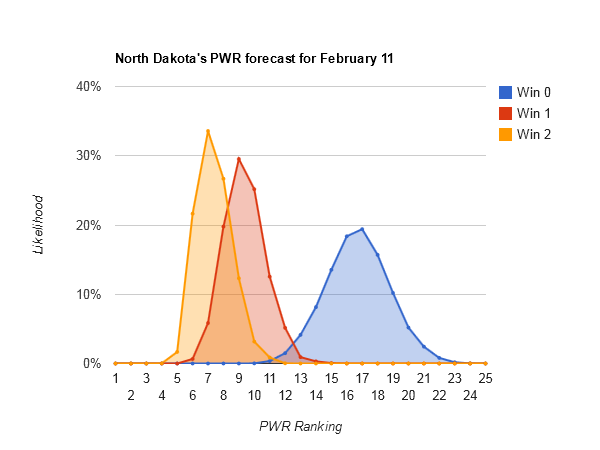
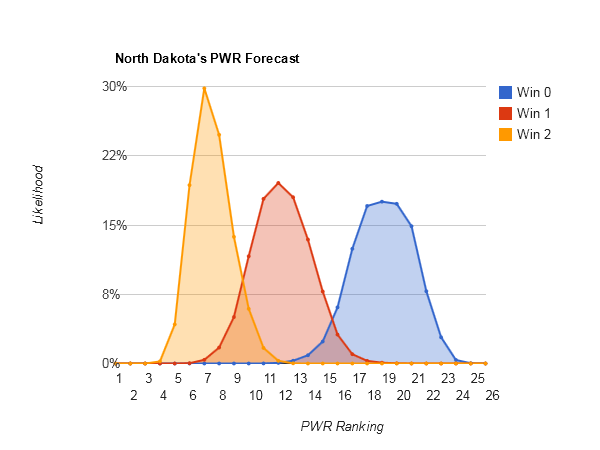
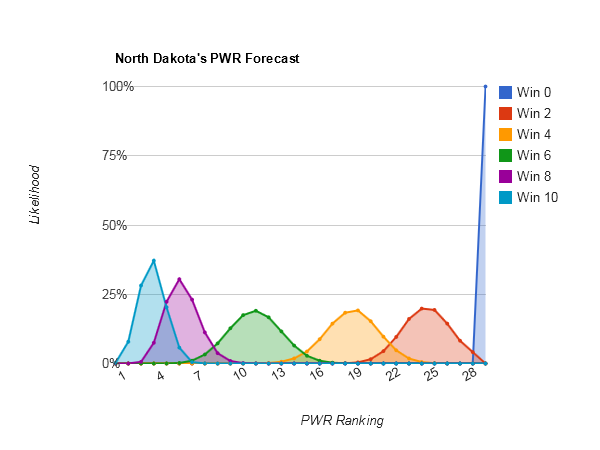
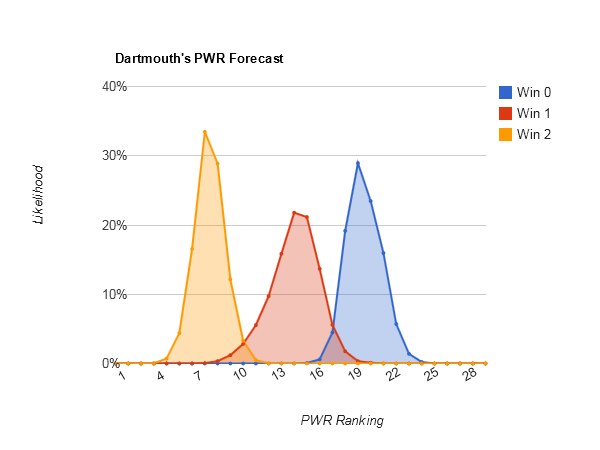
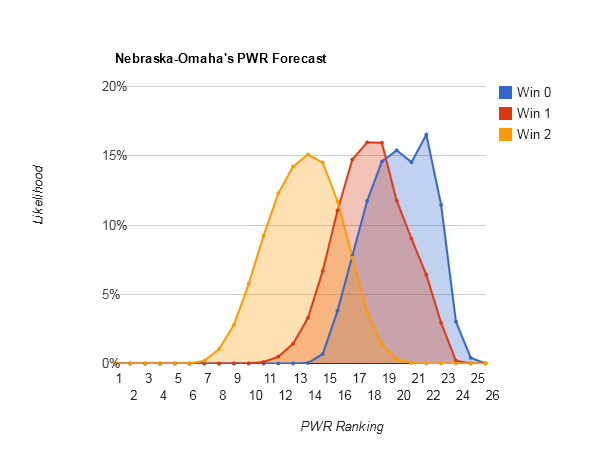
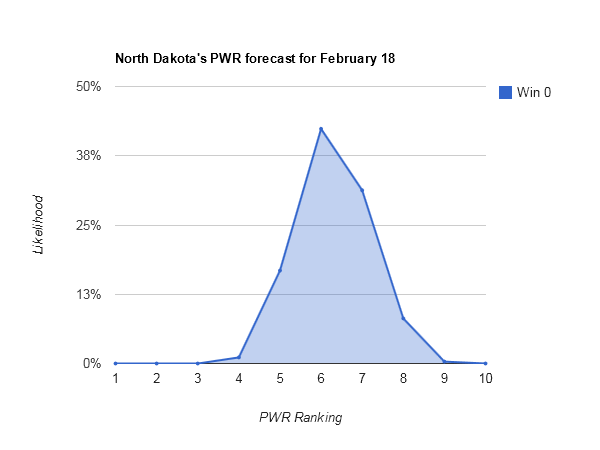
Idle #6 North Dakota could make some small moves in the Pairwise Rankings (PWR) this week, with anything between 5 and 8 being reasonably likely.

Key games for UND

Matchups that most affect UND’s PWR
Matchup Number
of wins		 Effect on
UND’s PWR
Ohio State over Western Michigan (1 of 2) 1.13
Ohio State over Western Michigan (2 of 2) 1.05

The reason those games (and others) are important can be deduced by studying the PWR comparison details for UND.

UND’s downside potential

Western Michigan is clearly the bigggest threat this week, with UND currently winning the comparison on the back of a very narrow .5470 to .5454 RPI lead.

Niagara is similarly knocking on the door, losing the comparison to UND only on the basis of Niagara’s RPI of .5381.

Finally, Yale could take the comparison with UND by defeating both Union and Rensselaer, thus raising their TUC record to .5667 (vs. UND’s .5470).

UND’s upside potential

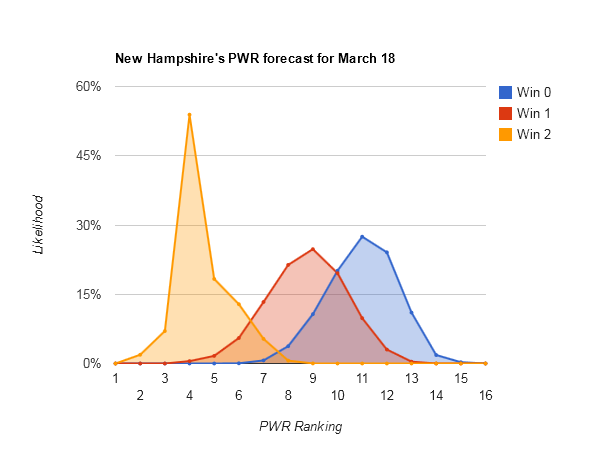
Though New Hampshire is winning the comparison to UND 3-0, two of those criteria would flip to UND if New Hampshire got swept. UND could take both RPI and TUC.

Other interesting teams this week

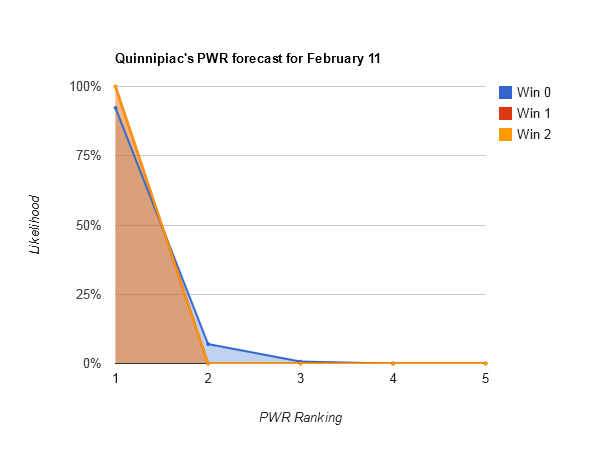
Smallest range of outcomes — #1 Quinnipiac (#1-#1). Sorry Gopher fans, not this week.

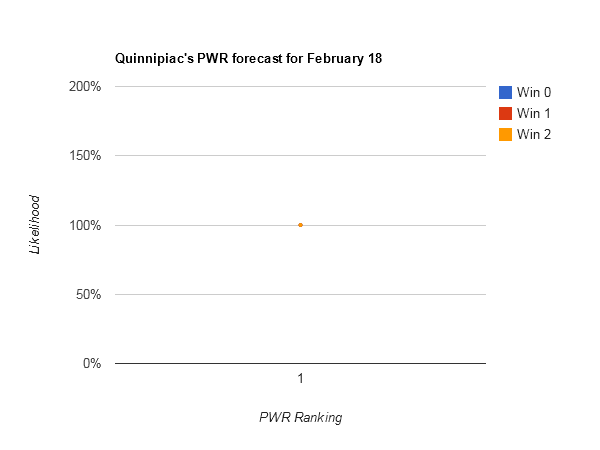
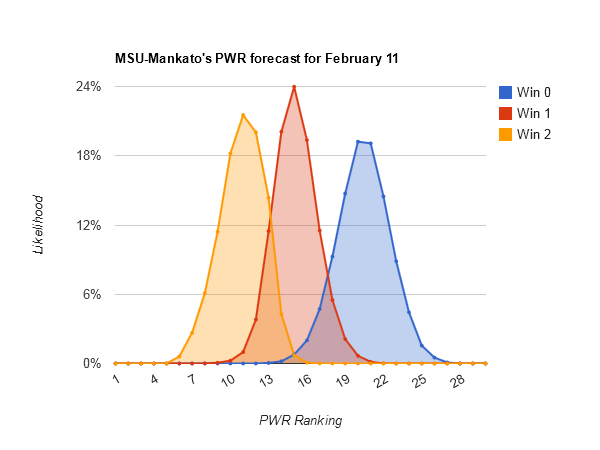
Of the teams that have a two comparison or less deficit with Quinnipiac [Quinnipiac PWR comparisons] (only North Dakota, MSU-Mankato, Niagara, Wisconsin, Providence, Holy Cross, and Robert Morris), none can hope to catch their RPI of .5885 any time soon.

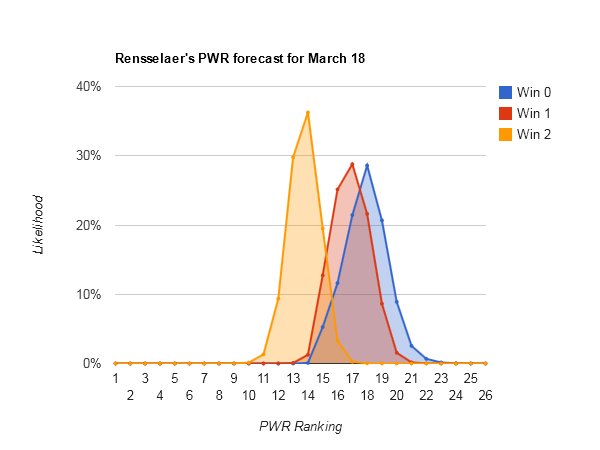
Largest range of outcomes — #23 Rensselaer (#13-#32), #25 Colgate (#13-#32), and #20 Merrimack (#12-#31)

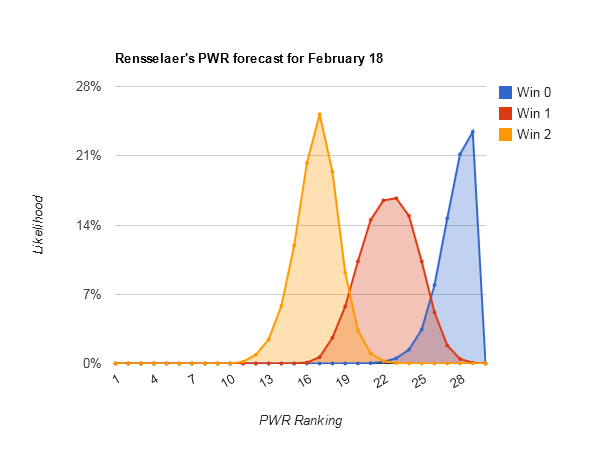
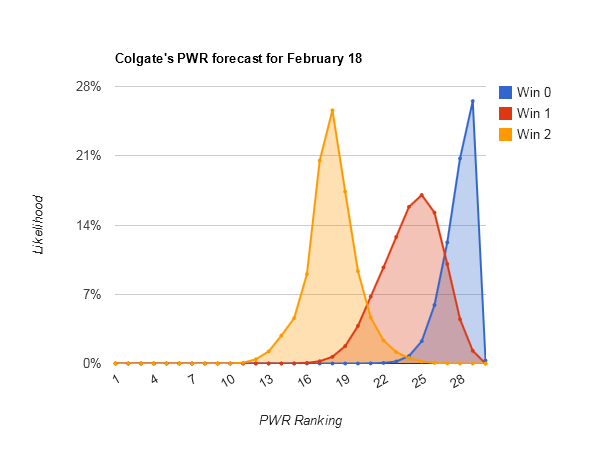
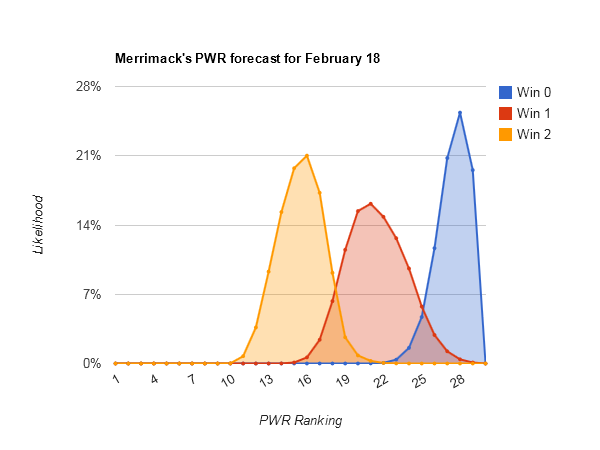
Looking at Rensselaer PWR comparisons, Colgate PWR comparisons, and Merrimack PWR comparisons, all have fairly middling RPIs in the .5100s and quite a few comparisons being decided by RPI. That creates a lot of opportunity for both upward and downward movement from that part of the comparison table.

Most upside potential — #31 Robert Morris (#16–non-TUC)

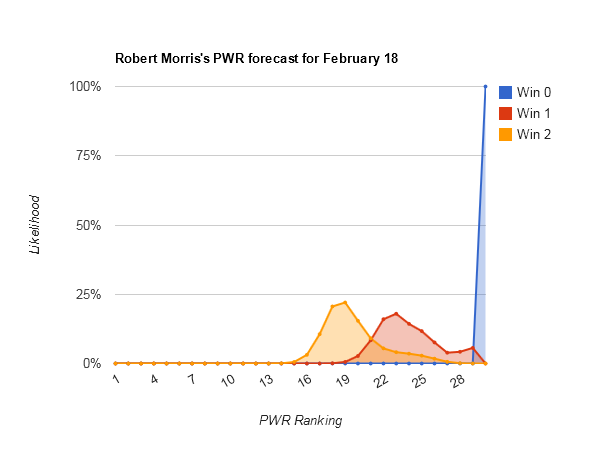
Robert Morris’s story is simple (Robert Morris PWR comparisons): The TUC criterion hasn’t come into play for them yet because they don’t have 10 games and a sweep this weekend (at least a win seems necessary to stay a TUC) would give them an impressive .700 record vs. TUCs. That would immediately flip a lot of the 1-1 comparisons, and some of the 0-2’s vs teams that Robert Morris can overtake on RPI.

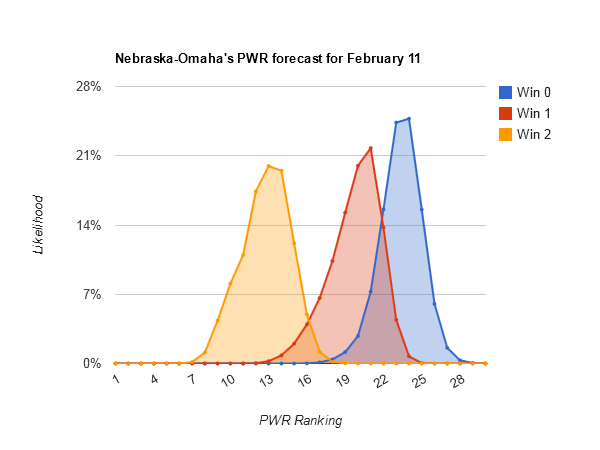
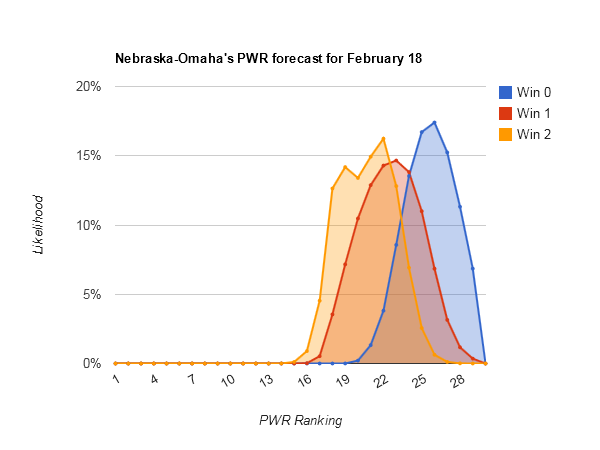
Most downside potential — #14 Dartmouth (#9-#27), #18 Nebraska-Omaha (#17-#31)

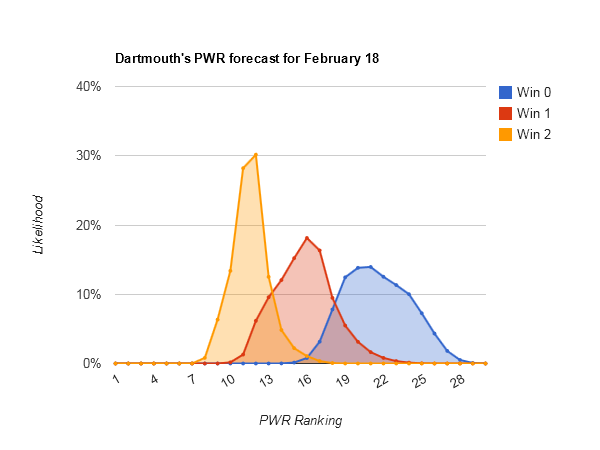
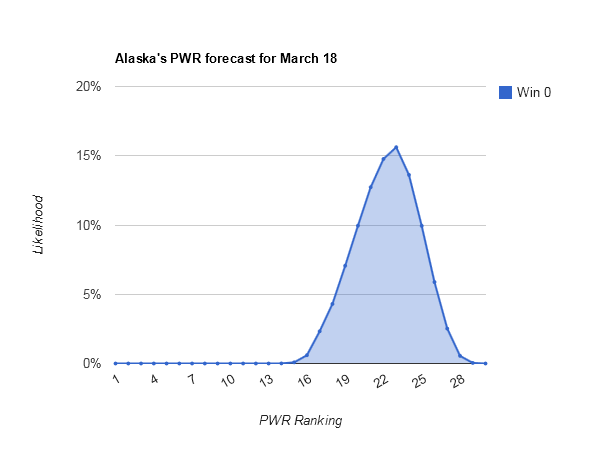
Dartmouth is tricky; just looking at Dartmouth’s PWR comparisons, it’s not immediately obvious why #14 Dartmouth has so much more downside potential than #15 Alaska [Alaska PWR comparisons], as RPIs and TUCs are similar. Fortunately, the simulations keep track of which games have the biggest effects on each teams, and there’s a valuable clue there:

Matchups that most affect Dartmouth’s PWR
Matchup Number
of wins		 Effect on
Dartmouth’s PWR
Dartmouth over Colgate   5.55
Dartmouth over Cornell   3.94
Brown over Rensselaer   1.56
Brown over Union   1.52
Miami over Notre Dame (2 of 2) 0.98
Lake Superior over Alaska (2 of 2) 0.84
Minnesota over Wisconsin (2 of 2) 0.80
Minnesota over Wisconsin (1 of 2) 0.61
Massachusetts over Mass.-Lowell (1 of 2) 0.58
Lake Superior over Alaska (1 of 2) 0.52
Robert Morris over Niagara (2 of 2) 0.51

The first thing that jumps out is how much Dartmouth wants Brown to win. It turns out that Brown is in danger of not being a TUC, and Dartmouth has 3 wins vs. Brown. Losing those wins would drop Dartmouth’s TUC record from .5333 to .4167. That gives Dartmouth significantly more downside potential with a couple losses than similarly ranked teams with similar RPIs.

Nebraska-Omaha [PWR comparisons], on the other hand, just has a miserable TUC of .3824. Alaska-Anchorage is a weak enough opponent that getting swept would push UNOs RPI from .5196 to about .5086. That would be enough on today’s RPI chart to drop UNO from #17 to #27 in RPI, certainly flipping a lot of comparisons given the poor TUC record. UNO seems to need a sweep not to fall.

Methodology

Each forecast is based on at least one million monte carlo simulations of the games in the described period. For each simulation, the PairWise Ranking (PWR) is calculated and the results tallied. The probabilities presented in the forecasts are the share of simulations in which a particular outcome occurred.

The outcome of each game in each simulation is determined by random draw, with the probability of victory for each team set by their relative KRACH ratings. So, if the simulation set included a contest between team A with KRACH 300 and team B with KRACH 100, team A will win the game in very close to 75% of the simulations. I don’t simulate ties or home ice advantage.

Resources

PWR forecasts for February 11

#10 North Dakota is facing another typical (for it) week of a little bit of upside potential if they sweep, but a fair amount of downside potential if they get swept. (Current PairWise Rankings)

Special Beanpot note — the simulations already include the results of this week’s Beanpot games, but forecast only through next Monday NOT including the Beanpot.

UND’s upside potential comes primarily from two games:

  • If Canisius sweeps Niagara, UND could take the RPI criterion and win the comparion with Niagara
  • If Minnesota sweeps St Cloud, UND could take the RPI criterion and win the comparison with St Cloud

(UND’s pairwise comparisons detailed)

Other teams of interest this week

Note that “likely” outcomes are those with a greater than 1% chance of occurring.

Team with the narrowest spread of likely outcomes: #1 Quinnipiac (#1-#2)

Team with the largest spread of likely outcomes: #19 Union (#9-#28)

Team with the most upside potential: #21 Nebraska-Omaha (#8-#27)

Team with the most downside potential: #12 MSU-Mankato (#7-#25)

Methodology

Each forecast is based on at least one million monte carlo simulations of the games in the described period. For each simulation, the PairWise Ranking (PWR) is calculated and the results tallied. The probabilities presented in the forecasts are the share of simulations in which a particular outcome occurred.

The outcome of each game in each simulation is determined by random draw, with the probability of victory for each team set by their relative KRACH ratings. So, if the simulation set included a contest between team A with KRACH 300 and team B with KRACH 100, team A will win the game in very close to 75% of the simulations. I don’t simulate ties or home ice advantage.

Resources

UND has opportunity to rise in rankings

#10 UND has fallen to a much more natural position in the Pairwise Rankings (PWR) than its lofty perch of the last couple weeks. If UND wins, its ranking goes up; it UND loses, its ranking goes down.

Follow up on last week’s predictions

In last week’s Weekly rankings analysis column I observed (and the outcomes were) that:

  • UND had more downside than upside and was likely to slump with anything less than a sweep. (Another one point weekend later, UND indeed fell from #6 to #10, right between the predicted win 1 and win 0 curves).
  • Mass.-Lowell similarly had more downside than upside, with only the comparison with UND as a possible gain and six comparisons as possible losses. (Mass.-Lowell took 3 of 4 points for the weekend and stayed #7 by taking the comparison with UND but losing the comparison with Miami).
  • Ferris St had big movement potential from #21 with a sweep or being swept (Ferris St split the weekend and dropped just one spot to #22).
  • Alaska had big movement potential from #18 (Alaska swept the weekend and climbed to #12, a much higher PWR than RPI).
  • Cornell had big movement potential from #22 (Cornell lost two and dropped to #27).
  • Dartmouth had the most downside potential from #9 (Dartmouth split the weekend and dropped to #15).

Bottom-line: this stuff works and reveals useful information that would be difficult to uncover browsing the comparison tables. But enough back-patting.

Whither UND?

In my first PWR post two weeks ago, I noted that UND was artificially high at #7 and needed to win about 6 of 14 remaining regular season games to finish in the at-large bid range of 13-15. UND has since gone 0-2-2 (.250) but dropped only to #10 in PWR.

UND still has a ton of downside potential if they continue to lose, but things are evening up a little with some upside potential for a sweep.

In the longer run view, the rough equivalent of 1 win has left UND needing about 5 wins in the remaining 10 games to be most likely to finish the regular season in the at-large bid range. Remember, though, that big moves can occur with a winning streak in the conference tournament.

Outcomes that most affect UND’s PWR this week
Outcome Average effect
on UND’s PWR
UND over Wisconsin (2 of 2) 11.57
UND over Wisconsin (1 of 2) 6.84
Holy Cross over Canisius (2 of 2) 1.74
Holy Cross over Canisius (1 of 2) 1.59
Minnesota-Duluth over Denver (2 of 2) 1.30
Michigan Tech over Nebraska-Omaha (2 of 2) 1.10
Minnesota-Duluth over Denver (1 of 2) 1.04
Michigan Tech over Nebraska-Omaha (1 of 2) 0.89
Bentley over Niagara (2 of 2) 0.76
Ferris St over Western Michigan (2 of 2) 0.71
Bentley over Niagara (1 of 2) 0.56
Rensselaer over Dartmouth 0.56

A lot of those are obvious with a quick glance at UND’s PWR comparisons.

  • Holy Cross is in danger of not being a TUC, but UND needs its 2 wins over the Crusaders to contribute to its mediocre record vs. TUCs (currently .500).
  • Denver could pass UND in RPI with a better weekend than North Dakota. Also, Duluth becoming a TUC seems to give UND a little juice (probably due to UND’s 1-0-1 record vs the Bulldogs, better than UND’s record vs current TUCs).
  • Nebraska-Omaha’s RPI could climb to about .539 with a sweep this weekend, which could allow them to take the comparison if UND also drops.
  • Similarly, Niagara and Dartmouth could take their comparisons with UND with a climb in RPI and a drop by UND.
  • Finally, UND barely loses the comparison with Western Michigan on the basis of RPI. Outperforming the Broncos this weekend would probably flip that.

Teams to watch

Biggest potential outcome (likelihood greater than 1%) spread of the week goes to UND (likely to come out between #5 and #23) and Dartmouth (likely to come out between #6 and #24).

Biggest upside potential goes to Nebraska-Omaha, which could climb a staggering 13 slots from #21 to #8 if everything went their way. This is mostly due to their reasonably strong RPI for a #21 team.

Biggest downside potential goes to Mass.-Lowell, which could drop 14 slots from #7 to #21 if everything went wrong. The looming disaster for Mass.-Lowell is clearly their miserable .250 TUC record coming into play when they hit 10 games vs. teams under consideration. It won’t happen this week without a little movement on the cliff (Maine isn’t a TUC), but it will eventually if they don’t gain some wins vs. TUCs.

Methodology

Each forecast is based on at least one million monte carlo simulations of the games in the described period. For each simulation, the PairWise Ranking (PWR) is calculated and the results tallied. The probabilities presented in the forecasts are the share of simulations in which a particular outcome occurred.

The outcome of each game in each simulation is determined by random draw, with the probability of victory for each team set by their relative KRACH ratings. So, if the simulation set included a contest between team A with KRACH 300 and team B with KRACH 100, team A will win the game in very close to 75% of the simulations. I don’t simulate ties or home ice advantage.

Resources