This is the last week we look at single week ranking probabilities, after this the “You are the Committee” calculators will go live and we’ll give you the rundown on all remaining possible outcomes.
It’s an interesting week, with a lot of teams’ fortunes still at play.
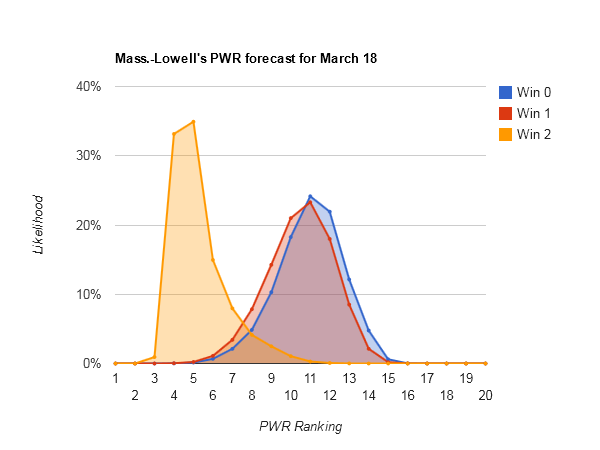
While the first three (#1 Quinnipiac, #2 Minnesota, and #3 Miami) in the Pairwise Rankings are reasonably secure, it starts to get interesting at #4 Mass.-Lowell. The Riverhawks are likely to stay #4-5 if they emerge from the best of 3, but plummet if they get eliminated.
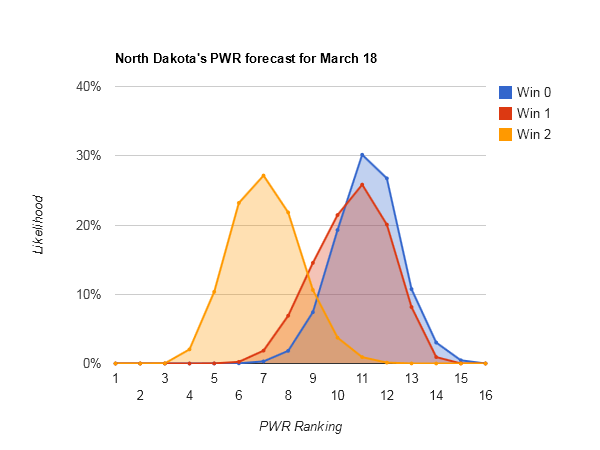
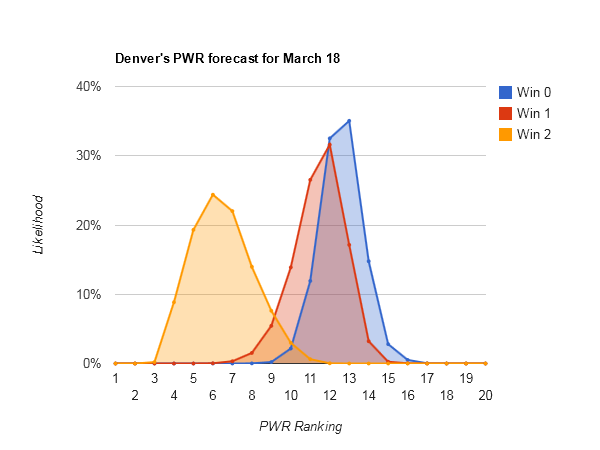
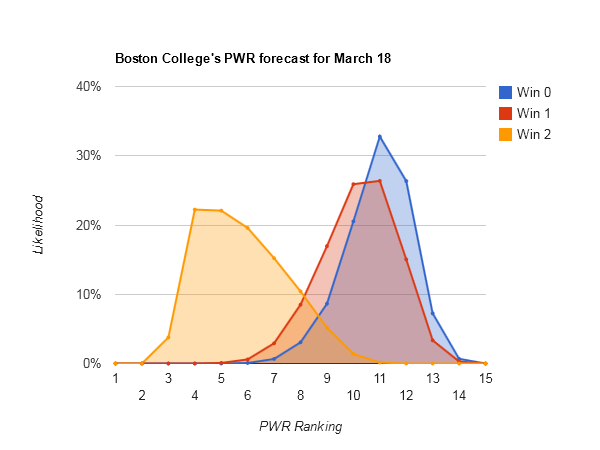
The same holds true for #5 North Dakota, #6 Denver, and #7 Boston College.
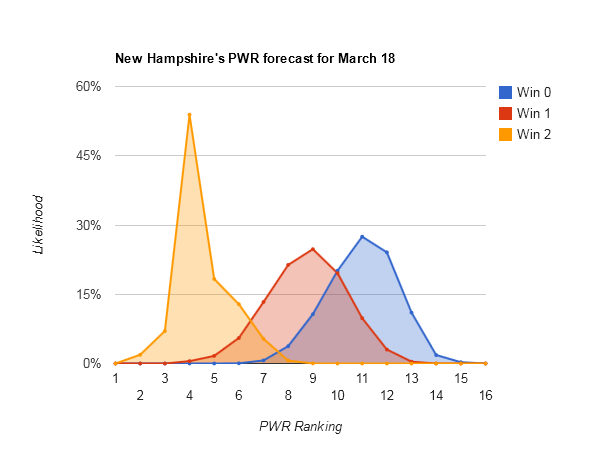
#8 New Hampshire is the first team with serious upside potential. It has a decent RPI and TUC record and is playing a fellow team under consideration, Providence. Most surprisingly, the Wildcats don’t drop much this weekend if they get eliminated (particularly if they win one).
#9 Mankato, #10 Western Michigan, #11 Yale, #12 St Cloud St, and #13 Niagara all have the opportunity to climb with success, or fall to the bubble if eliminated.
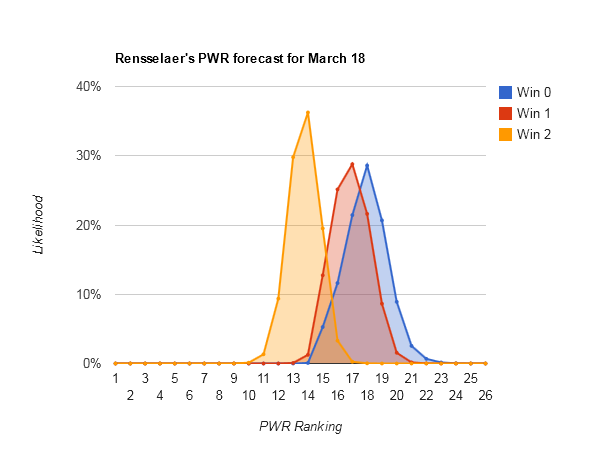
#14 Rensselaer is the highest ranked team that could fall definitively below the bubble if swept.
#15 Notre Dame, #16 Union, and #17 Boston University can all push themselves onto the bubble with success this weekend.
#18 Wisconsin can put itself into a good position but is unlikely to quite climb onto the bubble even with a sweep this weekend.
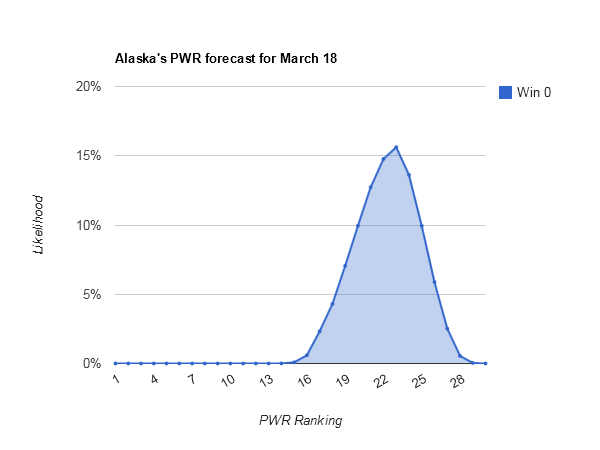
#22 Alaska is the highest ranked team not playing this weekend. Though incredibly unlikely (<1% chance), they could mathematically still climb onto the bubble.
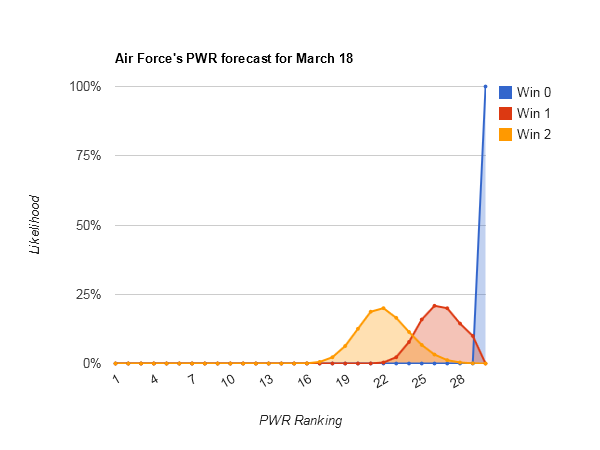
#25 Air Force is the cutoff beyond which even active teams don’t seem to be able to climb onto the bubble through this weekend’s performance alone.
If there’s anything else you’d like to know (e.g. what games are most important for a particular team, what are the chances for a team note listed here), just let me know in the comments!
Methodology
Each forecast is based on at least one million monte carlo simulations of the games in the described period. For each simulation, the PairWise Ranking (PWR) is calculated and the results tallied. The probabilities presented in the forecasts are the share of simulations in which a particular outcome occurred.
The outcome of each game in each simulation is determined by random draw, with the probability of victory for each team set by their relative KRACH ratings. So, if the simulation set included a contest between team A with KRACH 300 and team B with KRACH 100, team A will win the game in very close to 75% of the simulations. I don’t simulate ties or home ice advantage.
Resources
- Current PWR Rankings (SiouxSports.com)
- Current RPI Rankings (SiouxSports.com)
- CHN PWR Rankings (CollegeHockeyNews.com)
- TBRW build your own rankings (slack.net)
- Explanation of how PWR mimics NCAA tournament selection (CollegeHockeyNews.com)
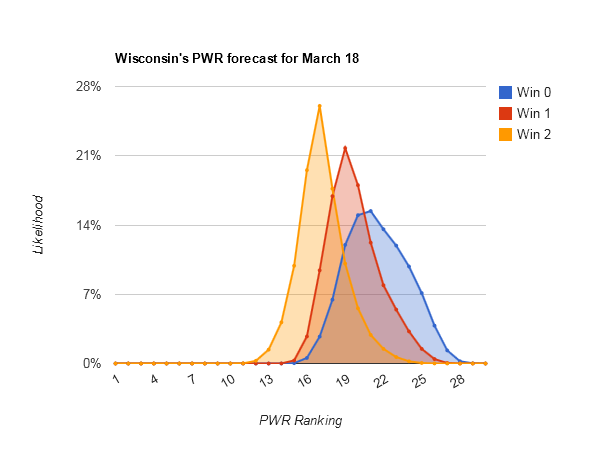
What is best for wisconsin? I assume CC dropping would be big.
First, obviously the Badgers need to sweep (though even just winning one
and getting eliminated does more to improve their ranking than getting
swept + any of the following).
Next important for this week,
Nebraska-Omaha over Mankato. While UNO winning the series is best, even
getting one win helps Wisconsin a lot. This is huge for two reasons:
trying to take the comparison with Mankato and keeping UNO a TUC.
Mankato
is currently winning the comparison with the Badgers, 4-3. So, one
point the other way gives it to Wisconsin. Gaining more than one win on
Mankato (e.g. Mankato goes 1-2, Wisconsin goes 2-1) should be enough for
Wisconsin to take the TUC criterion and the comparison.
UNO has a
meager .5051 RPI. A win keeps it above .500, a loss drops it below
(UNO
RPI details). Of course, those numbers are close enough to
.500 that things could shift based on other results. UNO being a TUC is
very important to Wisconsin as the Badgers are 2-0 vs. the Mavericks.
Losing them as a TUC would drop Wisconsin’s winning percentage vs. TUCs
from .475 to .417, enough to put at a minimum the comparison with Robert
Morris at risk.
Given its double impact, having UNO win even one
against Mankato is more important than the next, which is Denver
beating CC. Only a sweep here is useful because that’s what it takes to
push CC’s RPI below .500 and the Tigers out of being a TUC (CC
RPI details). CC dropping from being a TUC helps increase
UW’s winning percentage vs. TUCs from .475 to .528, enough to flip quite
a few TUC comparisons but only one head-to-head comparison this week,
Mankato. While this analysis is on the one week impact, all those
flipped TUC comparisons could make this series more important to the
Badgers in the long run if UW continues to win.
Remaining games
that help a bit this week — Air Force over Canisius (keeping Air Force a
TUC), Quinnipiac over Cornell (Cornell can be caught on RPI), Brown
over Rensselaer (Rensselaer can be caught on RPI), and New Hampshire
over Providence (Providence can be overtaken on RPI and TUC).
If BC, UNH, Mass/Lowell, Denver & ND all sweep Appears pairwise would look like this. BC3 UNH4 Mass/Lowell 5 Denver 6 Sioux 7.
Thank you for running these numbers. This is a great service to the college hockey fan community. It would be great if you would post the code you use to generate these numbers, but I certainly understand if you prefer to keep it to yourself. Thanks again!