Tag: PWR Rankings

UND needs wins to maintain its lofty ranking

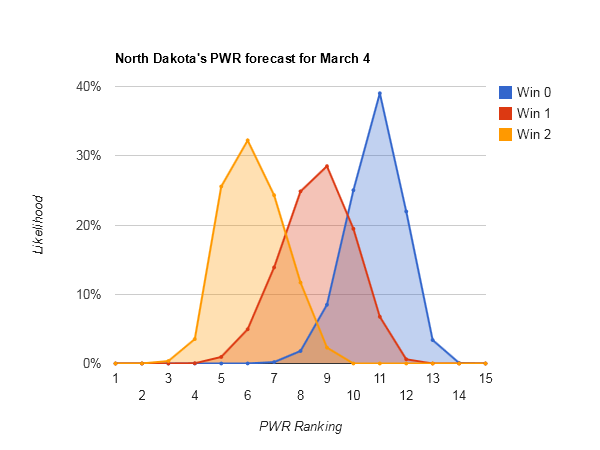
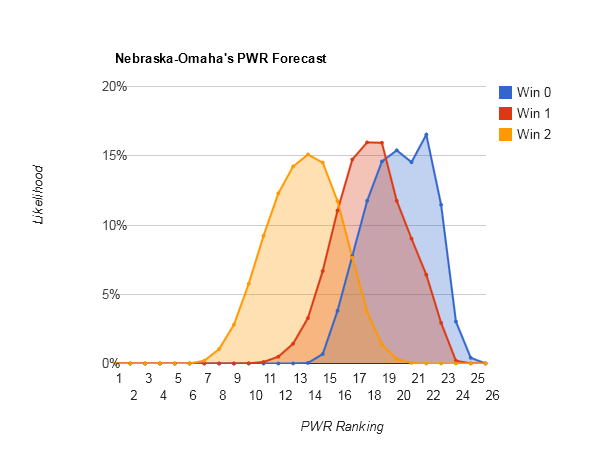
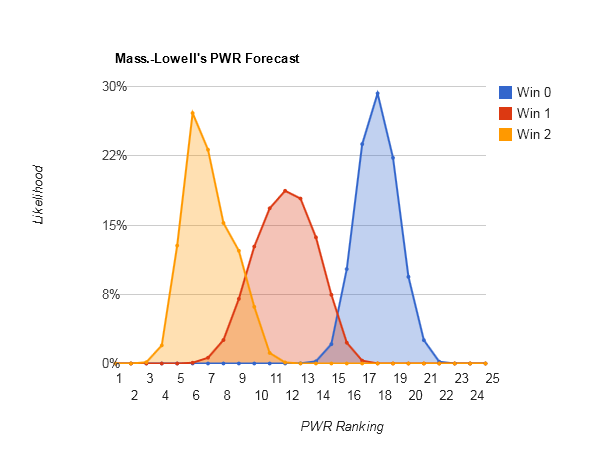
#5 UND has climbed its way back into needing a sweep this weekend just to maintain its current ranking (Current PWR rankings).

Looking at UND’s PWR comparison details, NoDak has very limited upside potential this week. Only the Boston College comparison is obviously within reach, but UND is already ahead of BC in the ranking because of the RPI tie-breaker, so flipping that comparison may not even result in a ranking increase.

UND’s PWR comparisons and RPI details reveal a significant downside, however. The RPI value of winning these games is only .5784, not significantly different enough from UND’s RPI of .5455 to budge it much. The RPI value of losing is .3284, enough to drag down UND’s RPI a fair amount. The PWR comparison details reveal that UND is winning a number of comparisons only by a slim RPI lead (Naigara .5427, Mass.-Lowell .5448, Western Michigan .5384, St Cloud St .5412, and Dartmouth .5216).

Weekend games with the largest effect on UND’s PWR:

Outcome Number of
games		 Average effect
on UND’s PWR
North Dakota over Bemidji State (2 of 2) 4.60
North Dakota over Bemidji State (1 of 2) 2.17
Merrimack over Mass.-Lowell (2 of 2) 1.05
Providence over Boston College (2 of 2) 1.05
Merrimack over Mass.-Lowell (1 of 2) 0.93
Air Force over Niagara (2 of 2) 0.92
Air Force over Niagara (1 of 2) 0.73
Alaska Anchorage over Alaska (2 of 2) 0.70

I did a minimum quick update on UND this week because I’m a little late and last week’s UND closes in on NCAA tournament berth was so comprehensive. However, if there’s anything else you’d like to see or any particular questions you have, just let me know!

Methodology

Each forecast is based on at least one million monte carlo simulations of the games in the described period. For each simulation, the PairWise Ranking (PWR) is calculated and the results tallied. The probabilities presented in the forecasts are the share of simulations in which a particular outcome occurred.

The outcome of each game in each simulation is determined by random draw, with the probability of victory for each team set by their relative KRACH ratings. So, if the simulation set included a contest between team A with KRACH 300 and team B with KRACH 100, team A will win the game in very close to 75% of the simulations. I don’t simulate ties or home ice advantage.

Resources

UND has opportunity to rise in rankings

#10 UND has fallen to a much more natural position in the Pairwise Rankings (PWR) than its lofty perch of the last couple weeks. If UND wins, its ranking goes up; it UND loses, its ranking goes down.

Follow up on last week’s predictions

In last week’s Weekly rankings analysis column I observed (and the outcomes were) that:

  • UND had more downside than upside and was likely to slump with anything less than a sweep. (Another one point weekend later, UND indeed fell from #6 to #10, right between the predicted win 1 and win 0 curves).
  • Mass.-Lowell similarly had more downside than upside, with only the comparison with UND as a possible gain and six comparisons as possible losses. (Mass.-Lowell took 3 of 4 points for the weekend and stayed #7 by taking the comparison with UND but losing the comparison with Miami).
  • Ferris St had big movement potential from #21 with a sweep or being swept (Ferris St split the weekend and dropped just one spot to #22).
  • Alaska had big movement potential from #18 (Alaska swept the weekend and climbed to #12, a much higher PWR than RPI).
  • Cornell had big movement potential from #22 (Cornell lost two and dropped to #27).
  • Dartmouth had the most downside potential from #9 (Dartmouth split the weekend and dropped to #15).

Bottom-line: this stuff works and reveals useful information that would be difficult to uncover browsing the comparison tables. But enough back-patting.

Whither UND?

In my first PWR post two weeks ago, I noted that UND was artificially high at #7 and needed to win about 6 of 14 remaining regular season games to finish in the at-large bid range of 13-15. UND has since gone 0-2-2 (.250) but dropped only to #10 in PWR.

UND still has a ton of downside potential if they continue to lose, but things are evening up a little with some upside potential for a sweep.

In the longer run view, the rough equivalent of 1 win has left UND needing about 5 wins in the remaining 10 games to be most likely to finish the regular season in the at-large bid range. Remember, though, that big moves can occur with a winning streak in the conference tournament.

Outcomes that most affect UND’s PWR this week
Outcome Average effect
on UND’s PWR
UND over Wisconsin (2 of 2) 11.57
UND over Wisconsin (1 of 2) 6.84
Holy Cross over Canisius (2 of 2) 1.74
Holy Cross over Canisius (1 of 2) 1.59
Minnesota-Duluth over Denver (2 of 2) 1.30
Michigan Tech over Nebraska-Omaha (2 of 2) 1.10
Minnesota-Duluth over Denver (1 of 2) 1.04
Michigan Tech over Nebraska-Omaha (1 of 2) 0.89
Bentley over Niagara (2 of 2) 0.76
Ferris St over Western Michigan (2 of 2) 0.71
Bentley over Niagara (1 of 2) 0.56
Rensselaer over Dartmouth 0.56

A lot of those are obvious with a quick glance at UND’s PWR comparisons.

  • Holy Cross is in danger of not being a TUC, but UND needs its 2 wins over the Crusaders to contribute to its mediocre record vs. TUCs (currently .500).
  • Denver could pass UND in RPI with a better weekend than North Dakota. Also, Duluth becoming a TUC seems to give UND a little juice (probably due to UND’s 1-0-1 record vs the Bulldogs, better than UND’s record vs current TUCs).
  • Nebraska-Omaha’s RPI could climb to about .539 with a sweep this weekend, which could allow them to take the comparison if UND also drops.
  • Similarly, Niagara and Dartmouth could take their comparisons with UND with a climb in RPI and a drop by UND.
  • Finally, UND barely loses the comparison with Western Michigan on the basis of RPI. Outperforming the Broncos this weekend would probably flip that.

Teams to watch

Biggest potential outcome (likelihood greater than 1%) spread of the week goes to UND (likely to come out between #5 and #23) and Dartmouth (likely to come out between #6 and #24).

Biggest upside potential goes to Nebraska-Omaha, which could climb a staggering 13 slots from #21 to #8 if everything went their way. This is mostly due to their reasonably strong RPI for a #21 team.

Biggest downside potential goes to Mass.-Lowell, which could drop 14 slots from #7 to #21 if everything went wrong. The looming disaster for Mass.-Lowell is clearly their miserable .250 TUC record coming into play when they hit 10 games vs. teams under consideration. It won’t happen this week without a little movement on the cliff (Maine isn’t a TUC), but it will eventually if they don’t gain some wins vs. TUCs.

Methodology

Each forecast is based on at least one million monte carlo simulations of the games in the described period. For each simulation, the PairWise Ranking (PWR) is calculated and the results tallied. The probabilities presented in the forecasts are the share of simulations in which a particular outcome occurred.

The outcome of each game in each simulation is determined by random draw, with the probability of victory for each team set by their relative KRACH ratings. So, if the simulation set included a contest between team A with KRACH 300 and team B with KRACH 100, team A will win the game in very close to 75% of the simulations. I don’t simulate ties or home ice advantage.

Resources