UND’s PWR rankings — a look ahead

Last week I gave a quick preview of UND’s PWR chances for the weekend. After a tie and a win, UND landed about where expected at #19. However, UND still has good upside potential.

UND’s one week outlook

A sweep should move UND solidly into “at large” position, while a split would leave UND about where it is (with a slight improvement a bit more likely than a slight fall).

UND’s regular season outlook

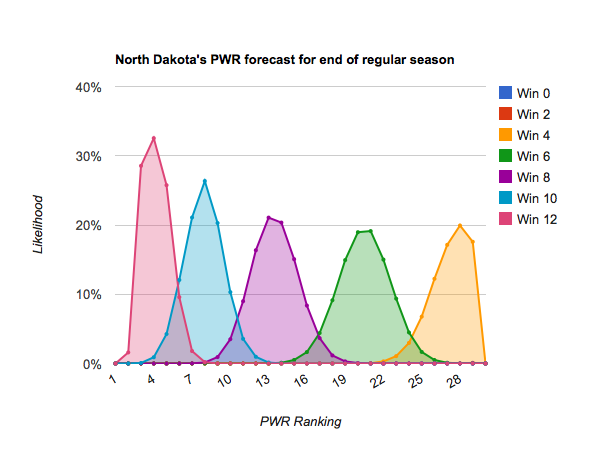
The bigger picture, though, is after UND’s phenomenal lossless streak, what do they need to do to finish in charge of their own destiny?

Winning 8 of its remaining 12 would put UND in a decent position to make the playoffs at large, while only winning 6 would likely leave UND in need of some conference tournament success.

More PWR analysis (non-UND teams)

I’m pleased to announce a new web site, College Hockey Ranked, to which I’ll (slowly) be migrating the non-UND hockey ranking information. This will allow SiouxSports to refocus more tightly on being a destination for UND fans, while CollegeHockeyRanked will try to appeal to a more general college hockey audience. UND fans who just want to read about UND won’t have to sift through as much information about other teams (except as it pertains to UND), non-UND fans who want more general analysis won’t have to skip over UND-centric analysis if they just visit that site, and of course anyone interested in both can simply follow both sites.

The immediate impact of this shift is that I’ll start posting my non-UND analysis to articles on that site. At least for this season, though, I’ll probably link between the two a lot.

Methodology

Each forecast is based on at least one million monte carlo simulations of the games in the described period. For each simulation, the PairWise Ranking (PWR) is calculated and the results tallied. The probabilities presented in the forecasts are the share of simulations in which a particular outcome occurred.

The outcome of each game in each simulation is determined by random draw, with the probability of victory for each team set by their relative KRACH ratings. So, if the simulation set included a contest between team A with KRACH 300 and team B with KRACH 100, team A will win the game in very close to 75% of the simulations. I don’t simulate ties or home ice advantage.

Resources

5 thoughts on “UND’s PWR rankings — a look ahead”

  2. I would also say that the ECAC and the Hockey East are going to beat up on each other as well. I remember one season, not too long ago when the WCHA had a lot teams high in the pairwise until the teams started beating up on each other. Do you think this will happen?

  3. Great question, Eric.

    I was going to try to do a piece on the NCHC’s chances, since there’s been a lot of commentary how they’ve underperformed. But maybe I can expand it to something about each conference’s overall potential.

Leave a Reply